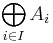Direct sum
 denotes direct sum; it is also the astrological and astronomical symbol for Earth, and a symbol for the Exclusive disjunction.
denotes direct sum; it is also the astrological and astronomical symbol for Earth, and a symbol for the Exclusive disjunction.In mathematics, one can often define a direct sum of objects already known, giving a new one. This is generally the Cartesian product of the underlying sets (or some subset of it), together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question. In cases where an object is expressed as a direct sum of subobjects, the direct sum can be referred to as an internal direct sum.
The direct sum of a family of objects Ai, with i ∈ I, is denoted by 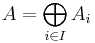 and each Ai is called a direct summand of A.
and each Ai is called a direct summand of A.
Examples include the direct sum of abelian groups, the direct sum of modules, the direct sum of rings, the direct sum of matrices, and the direct sum of topological spaces.
A related concept is that of the direct product, which is sometimes the same as the direct sum, but at other times can be entirely different.
Contents |
Direct sum of abelian groups
The direct sum of abelian groups is a prototypical example of a direct sum. Given two abelian groups (A, ∗) and (B, ·), their direct sum A ⊕ B is the same as their direct product, i.e. its underlying set is the Cartesian product A × B with the group operation ○ given componentwise:
- (a1, b1) ○ (a2, b2) = (a1 ∗ a2, b1 · b2).
This definition generalizes to direct sums of finitely many abelian groups.
For an infinite family of abelian groups Ai for i ∈ I, the direct sum
is a proper subgroup of the direct product. It consists of the elements 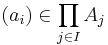 such that ai is the identity element of Ai for all but finitely many i.
such that ai is the identity element of Ai for all but finitely many i.
In this case, the direct sum is indeed the coproduct in the category of abelian groups.
Direct sum of modules (e.g. vector spaces)
Direct sum of representations
Group representations
The direct sum of group representations generalizes the direct sum of the underlying modules, adding a group action to it. Specifically, given a group G and two representations V and W of G (or, more generally, two G-modules), the direct sum of the representations is V ⊕ W with the action of g ∈ G given component-wise, i.e.
- g·(v, w) = (g·v, g·w).
Direct sum of rings
Given a finite family of rings R1, ..., Rn, the direct product of the Ri is sometimes called the direct sum.
Note that in the category of commutative rings, the direct sum is not the coproduct. Instead, the coproduct is the tensor product of rings.[1]
Internal direct sum
An internal direct sum is simply a direct sum of subobjects of an object.
For example, the real vector space R2 = {(x, y) : x, y ∈ R} is the direct sum of the x-axis {(x, 0) : x ∈ R} and the y-axis {(0, y) : y ∈ R}, and the sum of (x, 0) and (0, y) is the "internal" sum in the vector space R2; thus, this is an internal direct sum. More generally, given a vector space V and two subspaces U and W, V is the (internal) direct sum U ⊕ W if
- U + W = {u + w : u ∈ U, w ∈ W} = V, and
- if u + w = 0 with u ∈ U and w ∈ W, then u = w = 0.
In other words, every element of V can be written uniquely as the sum of an element in U with an element of W
Another case is that of abelian groups. For example, the Klein four-group V = {e, a, b, ab} is the (internal) direct sum of the cyclic subgroups <a> and <b>.
By contrast, a direct sum of two objects which are not subobjects of a common object is an external direct sum. Note however that "external direct sum" is also used to refer to an infinite direct sum of groups, to contrast with the (larger) direct product.
Notes
References
- Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR1878556